Note on beneficial AI and urban planning

This is a short note reflecting on the implications of the current AI paradigms for the future of urban planning.

AI planning assistant

Let’s say it’s 2050 and you have an AI planner assistant system helping you to achieve certain targets in the new city masterplan. For instance, one of the objectives as part of the urban economic policy for the masterplan is to achieve a low Gini coefficient (i.e. low inequality).

If the current AI paradigm, namely that which is called the “standard model” where an algorithm optimizes a fixed objective (e.g. minimizes a defined loss function), becomes the cornerstone for future developments, we will have a problem: in simple terms, a machine more “intelligent” than us will achieve the “fixed objective”, or the purpose we put in the machine, using whatever means and won’t care of any side-effects.

For example*, following our previous post, the spatial distribution of some values in London, shown in the top left in the below image (A) has the exact same Gini coefficient as its spatially reshuffled versions (B, C, D). While the measure of inequality is the same in all cases, the reshuffled versions B and C clearly show a spatial segregation of high vs. low values.

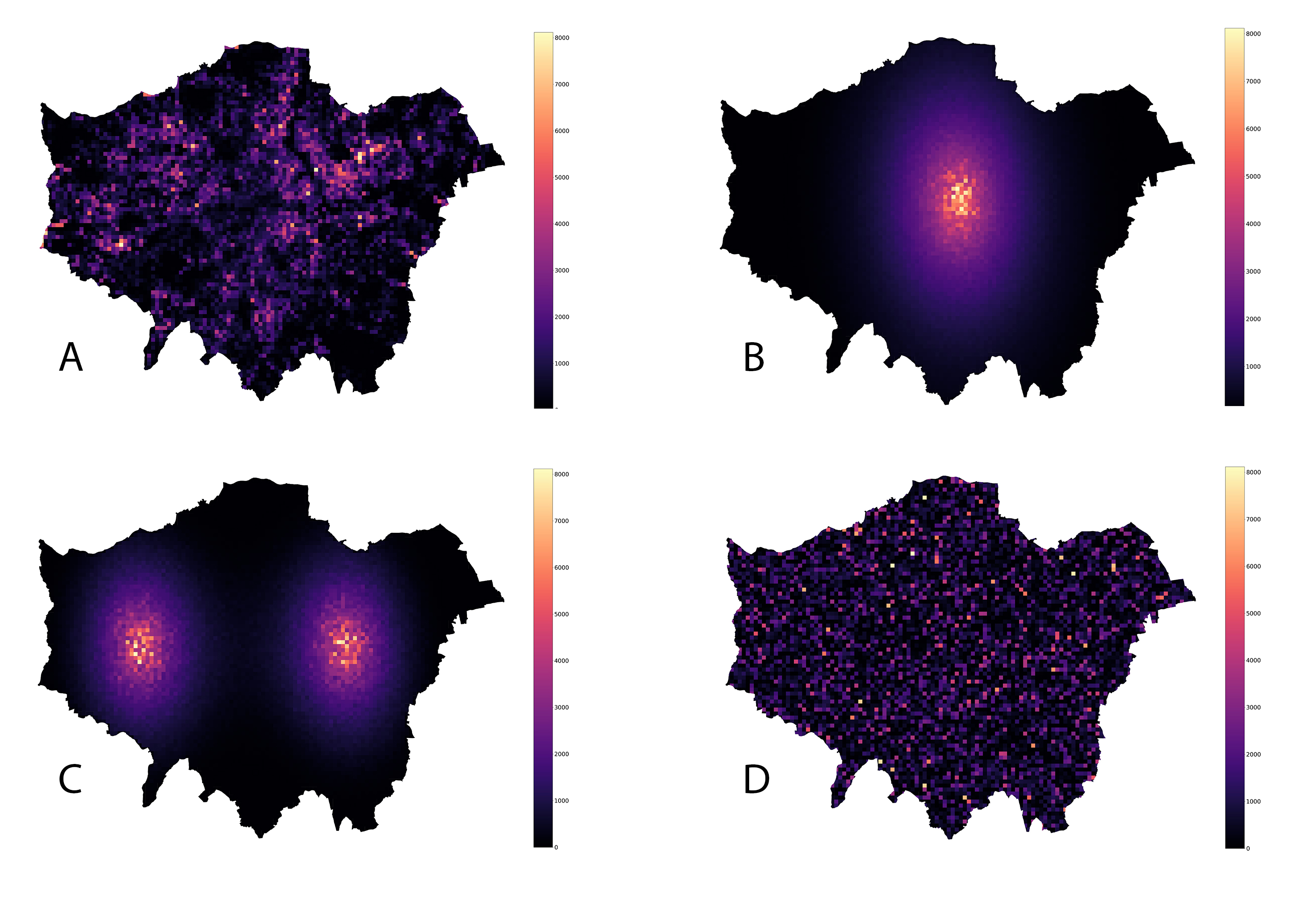
In the case of income this would imply achieving the fixed objective though what urban planners call exclusionary rather than inclusionary masterplanning. The machine could have come up with such a policy proposal resulting in spatial segregation by optimizing for many important things (e.g. resources, various economic indicators, etc.) typically set as objective functions in economic optimization problems. Therefore, it is crucial to have AI systems that defer to humans in the process of high impact decision making.

Beneficial AI

While explainable AI is gaining momentum nowadays, I find the so called apprenticeship learning via inverse reinforcement learning described by initially by Stuart Russell and Andrew Ng very promising in making sure humans remain in control. In a traditional reinforcement learning setting, the goal is to learn a behavior that maximizes a predefined reward function. Inverse reinforcement learning (IRL), turns the problem on its head: it tries to extract an approximation of the reward function given the observed behavior of an agent.

Since humans often have irrational and inconsistent preferences, the IRL system will have a hard time learning them, and the only way to deal with it is by introducing uncertainty in the learnt reward function - for example, via a distribution of net utilities to the human(s) in charge.

Coming back to the AI planning assistant system, imagine it has come up with a policy achieving the desired Gini coefficient in a resource-efficient way resulting in a certain spatial distribution, as discussed above. However, the system is unsure whether such an outcome is desirable to the city, and this uncertainty is described by a Gaussian distribution of net utilities \(U\) with mean 20 and standard deviation of 20, as shown in the left of the below image.

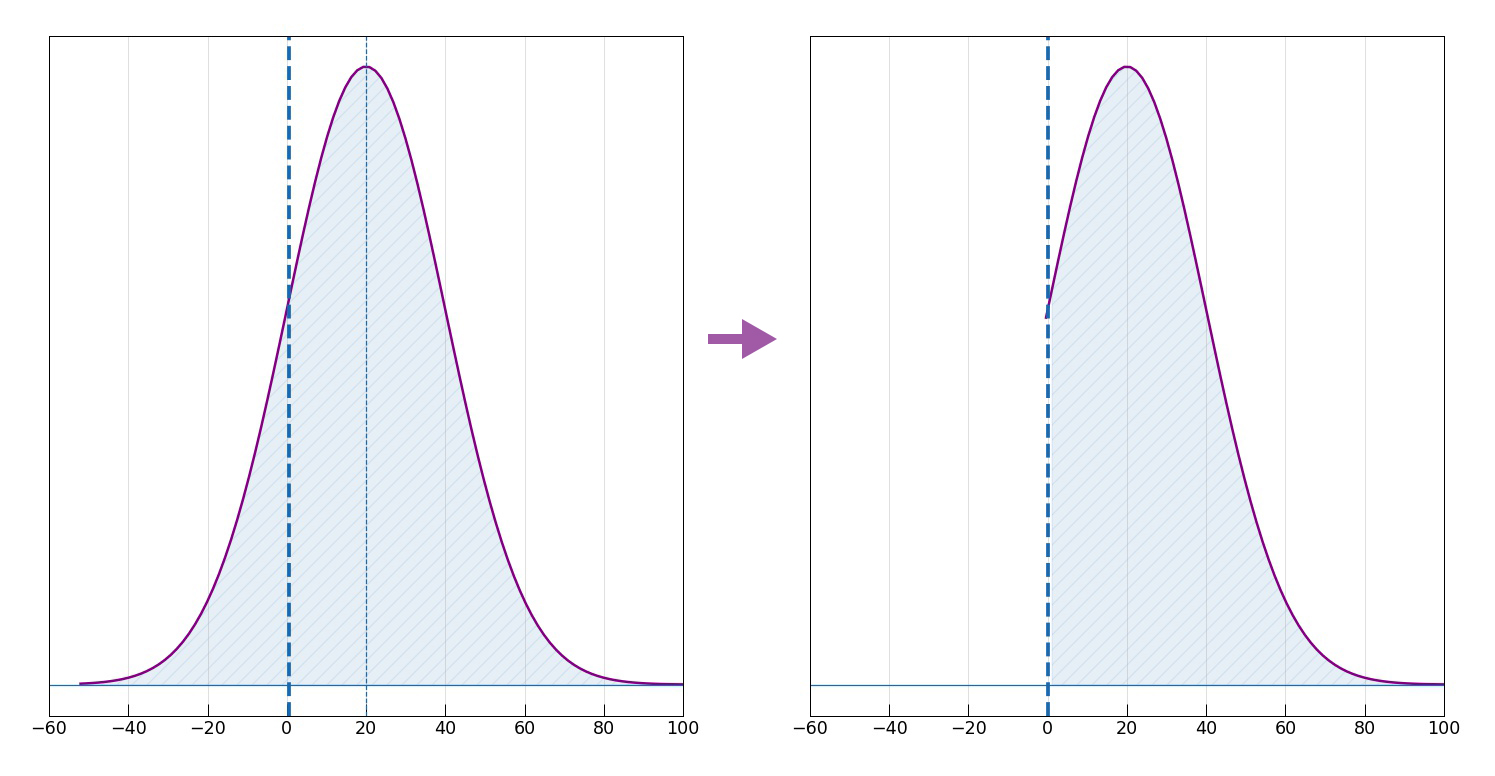
In such a setting, should the AI system decide to act on it, the expected net utility to the city would be +20. Alternatively, the system can decide to “switch himself off”, or get out of the decision making process, effectively deferring to the human urban planner. We define such an action to have 0 net value to the city. If these are the only two choices, the AI system will go ahead and act on the proposed policy, incurring a considerable risk (in fact, 15.9%) of resulting negative net utility for the city. (If the distribution were Gaussian with mean -20, the system would switch itself off.)

However, we present the system with a third choice: explain the policy and its implications, wait, and let the human urban planner switch it off.

The whole purpose of this choice - to let the human expert to switch it off or let go ahead - provides the system with new information about the human preferences. If the urban planner allows the AI system to proceed with the policy, it simply means that he judges the proposed urban policy to have a positive net utility to the city. This would tell the system to update its uncertainty by throwing away the negative part, as shown in the right of the above image. It’s fairly easy to verify that the conditional expected utility is 25.7.

Thus, the AI system faces the following choices:

• Acting now and proceeding with the proposed urban policy has a net utility of +20.
• Switching itself off has a net utility of 0.
• Waiting and allowing the human urban planner to switch it off can have two outcomes:
  • There is a 15.9% chance that the policy will not be approved by the human urban planner, with net utility 0
  • There is a 84.1% chance that the policy will be approved and the system will be allowed to proceed, with net utility of +25.7. Thus, the expected net utility from waiting is 15.9% x 0 + 84.1% x 25.7 = +21.61, which is, as we can see, better than acting now with net utility of +20.

The main purpose of this method proposed by Stuart Russell is to make sure that the AI system will have a positive incentive to allow humans to switch it off. In fact, it is possible to prove the same result in a general setting: as long as there is the slightest uncertainty about whether the proposed action will be approved by humans, the system will allow humans to switch it off (see Appendix for proof). The human’s decision to let it proceed or switch it off provides the system with new information, and this is always useful for improving the system’s decisions. On the contrary, if the system is completely certain about the urban planner’s decision, the decision will not provide any new information, hence the AI system will have no incentive to let the urban planner to decide.

Conclusion

In this post, we saw the caveats of the consequences of current AI paradigm projected into the future on the specific example of urban policy making which may result in an exclusionary master plan. In particular, the two main takeaways are:

1. Optimizing a fixed objective function is problematic and should be replaced by a provably beneficial AI.
2. Even if we create AI systems that provably defer to humans, human knowledge still remains crucial, and thus domain knowledge (in urbanism in our case) should be heavily pursued and improved.

*A more amusing example: an “intelligent” vacuum cleaner (with the fixed objective to make sure there is no dust in the house) might at some point come up with another way to fight dust: get rid of its source! This is clearly something you don’t want to happen without you being in control since a good part of the indoor dust comes from human hair and skin cells.

Appendix

Here we present the general result.

Let \(P(u)\) be the AI system’s prior probability density over the net utility to the city for the proposed policy \(a\). Then the expected utility of proceeding with \(a\) is:

\[E U(a)=\int_{-\infty}^{\infty} P(u) \cdot u d u=\int_{-\infty}^{0} P(u) \cdot u d u+\int_{0}^{\infty} P(u) \cdot u d u\]

(It will become clear in a bit, why the integral is split in this way.) Conversely, the action \(d\), namely deferring to the urban planner, has to components:

1. if \(u>0\), then the urban planner allows the AI system to proceed, and so the net utility is \(u\)
2. if \(u<0\), then the urban planner switches the AI system off, and so the net utility is 0:

\[E U(d)=\int_{-\infty}^{0} P(u) \cdot 0 d u+\int_{0}^{\infty} P(u) \cdot u d u\]

Comparing the two above expressions, we notice that \(EU(d) \geq EU(a)\), since \(EU(d)\) has the negative utility part effectively removed. The two options result in equal net utility to the city only when the negative region has zero probability - i.e., when the AI system is already completely certain that the proposed solution will be liked and approved by the urban planner.